3.1. Defining Integration#
In many of your mathematics courses to date, you have probably been exposed to integrals (especially, the popular Riemann integral). Here, we’re going to build up a more generic definition of an integral; that is, the ability to perform integration on any measurable space, rather than just Riemann ones. The way we’re going to do this is rather straightforward, and likely matches how your real analysis class built the Riemann integral: we’re going to start with the most basic of functions (simple functions), and demonstrate that these simple definitions obey desirable and intuitive rules for the integral to have. Then, we’re going to gradually relax this extremely simple operation to more and more complicated sorts of functions, until we have general rules for integration that will be sufficient for our treatment of probability theory.
3.1.1. Simple functions#
To build up integration rules, one of the most basic ways to do so is with something called simple functions:
Definition 3.1 (Simple function)
Suppose \((\Omega, \mathcal F)\) and \((\mathbb C, \Sigma)\) are measurable spaces, where \(\mu\) is a measure on \((\Omega, \mathcal F)\). A function \(\varphi \in m(\mathcal F, \Sigma)\) is said to be simple if, for disjoint sets \(\{F_n\}_{n \in [N]}\) are s.t. \(\mu(F_n) < \infty\) (that is, a \(\mu\)-finite sequence of disjoint measurable sets), then for all \(\omega \in \Omega\):
for a sequence \((\alpha_n)_{n \in [N]} \subseteq \mathbb C\).
Remember that since \(\varphi \in m(\mathcal F, \Sigma)\), then for any \(E \in \Sigma\), \(\varphi^{-1}(E) = \{\omega \in \Omega : \varphi(\omega) \in E\} \in \mathcal F\). The function need not have a unique representation to be simple; that is, the sets, and the coefficients, don’t necessarily have to be distinct. Let’s see an example:
Example 3.1 (Simple function is not unique)
Suppose that \(\Omega = [0, 1]\), and \(F_1 = [0, 0.5)\) and \(F_2 = [0.5, 1]\), and the measure \(\mu\) is the Lebesgue measure. note that \(F_1\) and \(F_2\) are a partition of \(\Omega\), and therefore disjoint, where \(\lambda(F_n) = 0.5 < \infty\). If \(\alpha_1 = 1\) and \(\alpha_2 = 2\), we could further split the disjoint sets into \(F_1' = [0, 0.25)\), \(F_2 = [0.25, 0.5)\), \(F_3' = [0.5, 0.75)\), and \(F_4' = [0.75, 1]\), where \(\alpha_1' = \alpha_2' = 1\), and \(\alpha_3' = \alpha_4' 2\). Here, \(\lambda(F_n') = 0.25 < \infty\). If \(\varphi(\omega) = \sum_{n \in [N]} \alpha_n \mathbb 1_{F_n}(\omega)\) and \(\varphi(\omega) = \sum_{n \in [N]} \alpha_n' \mathbb 1_{F_n'}(\omega)\), we can see that the representation is not unique, because \(\varphi(\omega) = \varphi'(\omega)\) for all \(\omega \in \Omega\).
We start by defining the integral of a simple function, rather intuitively:
Definition 3.2
Suppose that \(\varphi : (\Omega, \mathcal F) \rightarrow (\mathbb C, \Sigma)\) is a simple function, with corresponding coefficients/disjoint sets \(\{(\alpha_n, F_n)\}_{n \in [N]} \subseteq \mathbb C \times \Sigma\). We define the integral:
Conceptually, what is going on here is, we define the integral as an association with indicator functions, which we briefly touched on in the last chapter. The idea is that the “integral” of a single disjoint set is the “area” (measure) of the amount of “space” that each \(F_n\) occupies in \(\Omega\), and then we weight that by the corresponding coefficient \(\alpha_n\).
3.1.1.1. Properties of the integral for simple functions#
To show that the integral holds desirable properties, we need to extend a concept we defined previously: statements \(\mathcal S\) that are \(\mu\)-a.e. Remember that we defined this term in Definition 2.33. Recalling that definition, we can now extend this concept to a very particular set of statements, relations:
Definition 3.3 (Relation holds almost everywhere)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((S, \Sigma)\) is a measurable space. Assume that \(\varphi, \psi : (\Omega, \mathcal F) \rightarrow (S, \Sigma)\) are two functions. We say that a relation \(\rho : S \times S \rightarrow \{0, 1\}\) holds \(\mu\)-a.e. if there exists \(N \in \mathcal F\) s.t.:
and for every \(\omega \in \Omega \setminus N\), \(\rho\left(\varphi(\omega), \psi(\omega)\right) = 1\).
and we write that \(\rho(\varphi, \psi)\) is \(\mu\)-a.e. If the measure is implied, we shorten this to a.e.
The idea here is that for some subset of the \(\sigma\)-algebra of the domain, the relation does not hold, but that the measure of this set of points where the relation does not hold has measure \(0\). For every other point in the domain, the relation holds.
For instance, let’s take an example to be \(\rho(a, b) = a \geq b\) (a function which is true and returns \(1\) when \(a \geq b\), and false or returns \(0\) when \(a < b\)). Then \(\varphi \overset{a.e.}{\geq} \psi\) means that \(\mu\left(\left\{\omega \in \Omega : \varphi(\omega) < \psi(\omega)\right\}\right) = 0\). Let’s see how we can use this with the integral.
Intuitively, non-negative simple functions have non-negative integrals:
Property 3.1 (Non-negative simple function has non-negative integral)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measurable space. Suppose that \(\varphi : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) is a simple function. Then if \(\varphi \overset{a.e.}{\geq} 0\), \(\int \varphi\,\text d \mu \geq 0\).
Proof. If \(\varphi \overset{a.e.}{\geq} 0\) is simple, let:
be a (potentially non-unique) representation of it, which exists by Definition 3.1 as \(\varphi\) is simple.
Since \(\varphi \overset{a.e.}{\geq} 0\), then \(\alpha_n \geq 0\) for every \(n\) except a subset of indexing sets \(\mathcal M \subseteq [N]\), where for \(m \in \mathcal M\), \(\mu(F_m) = 0\). Then:
We can rescale simple functions by constants, and the integral of the rescaled function is just the rescaled integral:
Property 3.2 (Rescaling simple function has rescaled integral)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measurable space. Suppose that \(\varphi : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) is a simple function. For any \(r \in \mathbb R\), \(\int r\varphi \,\text d \mu = r\int \varphi \,\text d\mu\).
Proof. If \(\varphi\) is simple and \(r \in \mathbb R\), then:
So \(r\varphi\) is also simple with coefficients \(\{r\alpha_n\}_{n \in [N]}\).
Then:
Further, we can add simple functions and the integral of their sum is the sum of their integrals. This sounds rather trivial, but due to a slight amount of nuance, we need a new definition first. Notice that the subsets, \(\{F_n\}_{n \in [N]}\) of Definition 3.1 need not necessarily be a partition of \(\Omega\); we might be left with a set of points \(\Omega \setminus \bigsqcup_{n \in [N]} F_n\) where \(\omega \in N \Rightarrow \varphi(\omega) = 0\). This is the concept underlying the support of a function:
Definition 3.4 (Support of a function)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb C, \Sigma)\) is a measurable space, and \(f : (\Omega, \mathcal F) \rightarrow (\mathbb C, \Sigma)\) is a function. Then the support of \(f\) is:
Now, we can address the problem of integrating the sum of simple functions. To do so, we need a quick lemma: the sum of simple functions is simple:
Lemma 3.1 (Sum of simple functions is simple)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measurable space. Suppose that \(\varphi, \psi : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) are simple functions. Then \(\varphi + \psi\) is simple.
Proof. Since \(\varphi, \psi\) are simple, then:
We need to show that their sum is a simple function.
Problematically, \(\varphi\) and \(\psi\) might not have the same support; that is, \(\bigsqcup_{n \in [N]} A_n\) might not necessarily be \(\bigsqcup_{m \in [M]} B_m\).
Let \(A_0 \bigsqcup_{m \in [M]} B_m \setminus \bigsqcup_{n \in [N]}A_n\), and \(B_0 = \bigsqcup_{n \in [N]} A_n \setminus \bigsqcup_{m \in [M]}B_m\). Here, \(A_0\) is the set of all elements in \(\bigsqcup_{m \in [M]} B_m\) that are not in \(\bigsqcup_{n \in [N]} A_n\), and vice-versa. Note now that \(\bigsqcup_{m = 0}^M B_m = \bigsqcup_{n = 0}^N A_n\).
Since \(\{B_m\}_{m = 0}^M\) are still disjoint, then for every \(\omega \in A_n\), there exists one \(m \in \{0, ..., M\}\) where \(\omega \in B_m\) (and only one, since \(B_m\) are disjoint). Therefore, \(A_n = \bigsqcup_{m = 0}^M A_n \cap B_m\), and \(\mathbb 1_{\{A_n\}}(\omega) = \sum_{m = 0}^M \mathbb 1_{\{A_n \cap B_m\}}(\omega)\).
So:
and vice-versa for \(\psi(\omega)\).
Letting \(\alpha_0 = \beta_0 = 0\), then:
By construction, since \(\{A_n\}_n\) are mutually disjoint and \(\{B_m\}_m\) are mutually disjoint, that \(\{A_n \cap B_m\}_{n, m}\) are also mutually disjoint, so \(\varphi(\omega) + \psi(\omega)\) is simple.
and we are ready to address the quantity of interest:
Property 3.3 (Summing simple functions have summed integral)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measurable space. Suppose that \(\varphi, \psi : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) are simple functions. Then \(\int(\varphi : \psi) \,\text d \mu = \int \varphi \,\text d \mu + \int \psi \,\text d \mu\).
Proof. Let \(A_0, B_0, \alpha_0, \beta_0\) be defined as in Lemma 3.1. Then:
Observe that since \(\bigsqcup_{m = 0}^MB_m \supseteq A_n\) and for some \(n\) that \(\bigsqcup_{m = 0}^M \{A_n \cap B_m\} = A_n\), that \(\sum_{m = 0}^M \mu(A_n \cap B_m) = \mu(A_n)\), by countable additivity Definition 2.23. Then:
Using only these three foundational properties, we will be able to extend the extremely trivial concept of an integral that we outlined in Definition 3.2 to much more complicated functions. Let’s move to some corollaries of integration.
3.1.2. Corollaries of integration#
If these three properties hold for some class of functions, we obtain (for free) three more desirable results of integration. Notice that these results do not make any statements about the functions being simple; they just assume that the functions are in a class of functions where some of the properties we just discussed hold. This means we can pre-prepare some corollaries of integration wherein, if we can define other classes of functions in which those properties also hold, these corollaries will extend to those classes of functions, too:
Corollary 3.1 (Integration preserves inequalities)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measurable space. Suppose that \(\varphi, \psi : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) are in classes of functions which preserve non-negativity, summation, and rescaling by \(-1\) under integration. Then if \(\varphi \overset{a.e.}{\leq} \psi\), \(\int \varphi\,\text d \mu \leq \int \psi \,\text d \mu\).
Proof. Since integration preserves summation and rescaling (here, by \(-1\)) by supposition, then:
Note that if \(\varphi \overset{a.e.}{\leq} \psi\), then \(\psi - \varphi \overset{a.e.}{\geq} 0\), so \(\int (\psi - \varphi) \,\text d \mu \geq 0\), by the non-negativity property. Then:
Using the inequality preservation, we obtain equality preservation, too:
Corollary 3.2 (Integration preserves equality)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measurable space. Suppose that \(\varphi, \psi : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) are in classes of functions which preserve non-negativity, summation, and rescaling by \(-1\) under integration. Then if \(\varphi \overset{a.e.}{=} \psi\), \(\int \varphi\,\text d \mu = \int \psi \,\text d \mu\).
Proof. Note that since \(\varphi \overset{a.e.}{=} \psi\), that \(\varphi \overset{a.e.}{\leq} \psi\) and \(\varphi \overset{a.e.}{\geq} \psi\).
Then by Corollary 3.1:
Together, these two statements imply:
Finally, the inequality preservation also gives us an intuitive result for absolute values:
Corollary 3.3 (Absolute value upper bounds)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measurable space. Suppose that \(\varphi : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) is in a class of functions which preserve non-negativity, summation, and rescaling by \(-1\) under integration. Then:
Proof. By definition of \(|\cdot|\) (the absolute value), note that for every \(\omega \in \Omega\), \(\varphi(\omega) \leq |\varphi(\omega)|\), so \(\varphi \leq |\varphi|\) in absolute terms (and consequently, also almost everywhere; e.g., \(\varphi \overset{a.e.}{\leq} |\varphi|\), since absolute inequality is stronger than almost everywhere inequality).
Then by Corollary 3.1:
Further, note that \(-\varphi \leq |\varphi|\) (both absolutely and a.e.), so:
where the last line follows, also by Corollary 3.1.
Recalling that \(|y| = y \vee -y\), then:
Remember that \(a \wedge b\) notationally means \(\min(a, b)\), and \(a \vee b\) notationally means \(\max(a, b)\), so \(|y| = y \vee -y \equiv \max(y, -y)\) is just another way to write the absolute value.
We can use these properties of integrals of simple functions, as well as the corollaries, to show that integration can be defined for more complicated functions, too. Let’s try bounded functions.
3.1.3. Bounded functions#
The idea behind a bounded function is basically just that the function has an upper bound. You are probably pretty familiar with this idea from real analysis, so we’ll just define it formally here for you:
Definition 3.5 (Bounded function)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space and \((\mathbb C, \Sigma)\) is a measurable space. A function \(f \in m(\mathcal F, \Sigma)\) is called bounded if there exists \(M \in \mathbb R\) s.t. for any \(\omega \in \Omega\), \(|f(\omega)| \leq M\). For such a function, we write \(|f| \leq M\).
As it turns out, we can approximate the integral of bounded functions using simple functions. Basically, the idea is that we will use simple functions that approximate the bounded function from above, and then simple functions that approximate the bounded function from below. As we make the simple functions sequentially closer and closer approximations (from above and below) of our bounded function, the integrals of the simple functions we are using converge. We can then use the quantity these simple functions converge to as the integral of the bounded function. Since we already have integrals of simple functions, this quantity they converge to (from above and below) is therefore a well-defined quantity (it exists), and can be taken to be the integral of the bounded function:
Theorem 3.1 (Bounded functions can be approximated by simple functions)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measurable space. Suppose that \(\varphi, \psi : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) are in the class of simple functions, and \(f : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) is a bounded function. Suppose further that \(E \subseteq \Omega\) is a subset s.t. \(\mu(E) < \infty\), and for any \(\omega \in E^c\), \(f(\omega) = 0\) (\(f\) vanishes on \(E^c\)). Then:
Proof. Suppose that \(\varphi, \psi\) vanish on \(E^c\), and that \(f\) is bounded by \(M \in \mathbb R\).
First, we need to show that the sets of these simple functions \(\psi : \psi \geq f\) and \(\varphi : \varphi \leq f\) are non-empty. Letting \(\psi(\omega) = M\) and \(\varphi(\omega) = -M\) on \(E\) gives the desired result.
Recall that it suffices to show that if \(\sup_{\varphi \leq f} \int \varphi \,\text d \mu = \inf_{\psi \geq f}\int \psi \,\text d \mu\), then by the sandwich theorem as \(\varphi \leq f \leq \psi\), the desired result holds.
We will show the desired result in two steps:
1. \(\sup_{\varphi \leq f} \int \varphi \,\text d \mu \leq \inf_{\psi \geq f} \int \psi \,\text d \mu\):
Since \(\varphi \leq f \leq \psi\) for all \(\varphi, \psi\) that the supremum/infimum are being considered with respect to absolutely, then \(\varphi \leq \psi\) absolutely (and hence also a.e., since absolute inequality is stronger than a.e. inequality).
As \(\varphi, \psi\) are simple (and simple functions preserve non-negativity and summation properties of integration), the desired result holds by Corollary 3.1.
2. \(\sup_{\varphi \leq f} \int \varphi \,\text d \mu \geq \inf_{\psi \geq f} \int \psi \,\text d \mu\):
For each \(k \in \mathbb Z\) where \(-n + 1 \leq k \leq n\), let:
See Fig. 3.1 for details, and note that by construction, \(\varphi_n, \psi_n\) are simple functions. By construction, for each \(n \in \mathbb N\), that \(\bigsqcup_k E_{n,k} = E\), and further, \(\psi_n(\omega) - \varphi_n(\omega) = \frac{M}{n}\mathbb 1_{\{E\}}(\omega)\) (since the equality is absolute, it also holds a.e.), so by Corollary 3.2:
Further, since simple functions preserve summation by Property 3.3 and rescaling by \(-1\) by Property 3.2, then:
As \(\varphi_n(\omega) \leq f(\omega) \leq \psi_n(\omega)\) by construction, then by Property 3.3, and noting that as \(\varphi_n \in \{\varphi : \varphi \leq f,\varphi \text{ is simple}\}\) and \(\psi_n \in \{\varphi : \varphi \geq f,\psi \text{ is simple}\}\), then for all \(n\):
which follows because \(\mu(E)\) and \(M\) are fixed while \(n \rightarrow \infty\).
Then by the sandwich theorem since \(\varphi \leq f \leq \psi\):
To break this proof down a little bit, let’s take a look at this figure, which explains conceptually what’s going on:
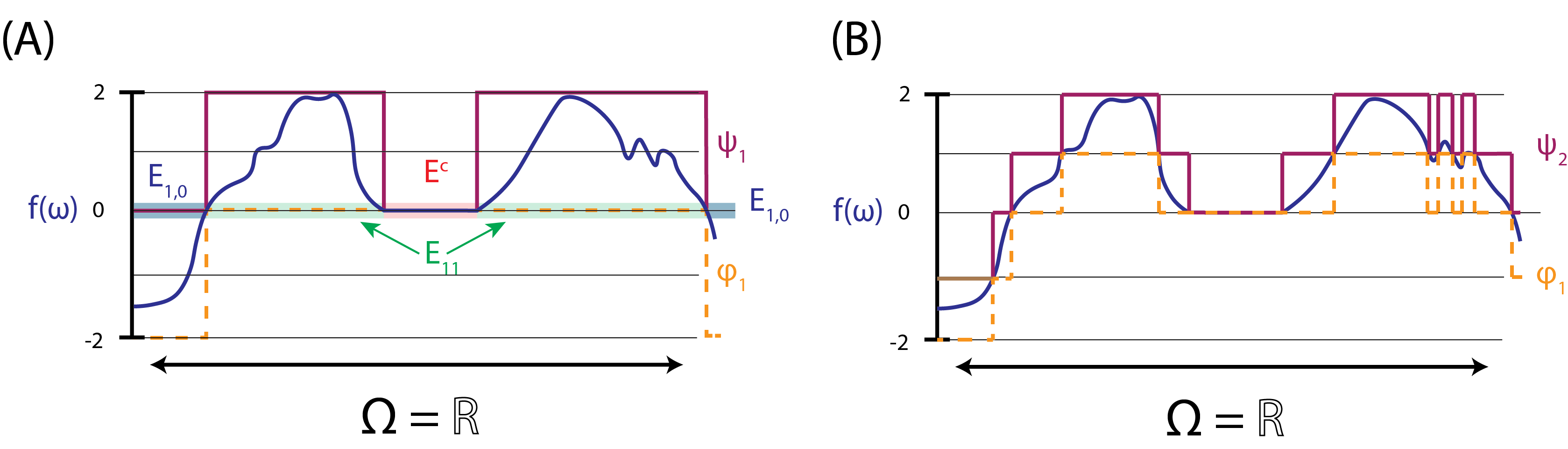
Fig. 3.1 (A) the function \(f(\omega)\) is shown in blue, where \(f : \mathbb R \rightarrow \mathbb R\) is bounded by \(M = 2\) (that is, \(|f| \leq 2\)). The sample space is split into three subsets, where \(E^c\) (shaded red box) is the vanishing subset, and the non-vanishing portions are \(E_{1,0}\) (shaded blue box) and \(E_{1,1}\) (shaded green box). The non-vanishing subset must have finite measure. \(\psi_1\) and \(\varphi_1\) are simple functions defined as in the proof. (B) we repeat this process, for \(n=2\). As \(n\) increases, the simple functions become more and more complex, providing better and better approximations of \(f\), from above (\(\psi_n\)) and below (\(\varphi_n\)).#
Since we pre-supposed that we had finite measure for the non-vanishing subset, the integrals for these simple functions \(\varphi_n\) and \(\psi_n\) will be well-defined quantities, because they form a partition of the non-vanishing subset (and hence, individually, their measures will be finite as well, which satisfies the assumption in Definition 3.1 for them to be simple functions).
3.1.3.1. Properties of the integral for bounded functions#
When functions are bounded on a finite non-vanishing measurable subset of the event space, we can extend all of the properties that we found with simple functions directly to bounded functions. Note that we are going to, in effect, use the fact that we defined the integral as in Theorem 3.1 as a supremum/infimum of simple functions, and just “borrow” the properties we learned about integrals for simple functions to show the results we want. Let’s get started:
Property 3.4 (Non-negative bounded function has non-negative integral)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f \in m(\mathcal F, \Sigma)\) is a bounded function that vanishes on a set \(E^c\), where \(\mu(E) < \infty\). Then if \(f \overset{a.e.}{\geq} 0\), \(\int f \,\text d \mu \geq 0\).
Proof. Let \(F \in \mathcal F\) be the set on which \(f \geq 0\). Let \(\varphi_0(\omega) = 0\) for every \(\omega \in F\), and let \(\varphi_0(\omega) = -M\) for every \(\omega \in F^c\), which is a simple function. Since \(f \overset{a.e.}{\geq} 0\), then \(\mu(F^c) = 0\).
Since \(\varphi_0\) is simple, then by Definition 3.2:
Note that \(\varphi_0 \in \{\varphi : \varphi \leq f, \varphi\text{ is simple}\}\) from the supremum condition Theorem 3.1, so:
because the supremum might be over other simple functions as well.
So what we did here was, we defined a simple function (the zero function) for the entire part of the sample space on which \(f \geq 0\), and set its other values using the bound on \(f\) to definitively obtain a simple function that is \(\leq f\). Then, we used that the supremum would be at least as large as the integral of one of the member functions to establish the appropriate bound.
Property 3.5 (Rescaled bounded function has rescaled integral)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) is a bounded function that vanishes on a set \(E^c\), where \(\mu(E) < \infty\). Then if \(r \in \mathbb R\), \(\int r f \,\text d \mu = r\int f \,\text d \mu\).
Proof. Suppose WOLOG that \(r > 0\). Then \(r \varphi \leq r f \iff \varphi \leq f\), and consequently by Theorem 3.1:
which is because \(\varphi\) are simple, and by Property 3.2. Then:
which is by Theorem 3.1.
Property 3.6 (Summed bounded functions have summed integrals)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f,g : (\Omega, \mathcal F) \rightarrow (\mathbb R, \Sigma)\) are bounded functions that vanishes on a set \(E^c\), where \(\mu(E) < \infty\). Then \(\int (f + g)\,\text d \mu = \int f \,\text d \mu + \int g \,\text d \mu\).
Proof. Note that if \(\psi_1 \geq f\) and \(\psi_2 \geq g\), then \(\psi_1 + \psi_2 \geq f + g\). Further, note that \(\{\psi : \psi \geq f + g\} \subseteq \{ \psi_1 + \psi_2 : \psi_1 \geq f, \psi_2 \geq g\}\). Consequently:
which is by Property 3.3 since \(\psi_1, \psi_2\) are simple. Continuing:
Repeating the same argument on \(-f\) and \(-g\), we obtain:
which is by rescaling by \(-1\) from Property 3.5. Combining (3.1) and (3.2):
Notice that since bounded functions obey inequalities with respect to \(0\), are rescalable by \(-1\), and their sums have summed integrals, that we obtain all of the integration corollaries in Section 3.1.2 for free!
3.1.4. Non-negative functions#
Next, we’re going to extend our repetoire of functions with well-defined integrals to the non-negative functions:
Definition 3.6 (Non-negative function)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measure space. A function \(f \in m(\mathcal F, \Sigma)\) is called non-negative if for every \(\omega \in \Omega\), \(f(\omega) \geq 0\). If \(f\) is a non-negative function, we write \(f \geq 0\).
To begin to define the integral of a non-negative function, we need to be able to integrate over sets:
Definition 3.7 (Integral over a set)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f \in m(\mathcal F, \Sigma)\). The integral over a set \(E \in \mathcal F\) is:
Now, we are ready to define the integral of a non-negative function:
Definition 3.8 (Integral of a non-negative function)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measure space, and a function \(f \in m(\mathcal F, \Sigma)\) is s.t. \(f \geq 0\). Then:
As we can see, this quantity is clearly well-defined (it contains at least one element): simply take \(h(\omega) = 0\) for all \(\omega \in \Omega\). Further, it is the supremum of the integrals of bounded functions, so it also could be non-finite. To calculate the integral of a bounded function, remember we just introduced a method of computing the integral from simple functions which approximated \(f\) from above and below. As we made these coarse simple functions more fine, their integrals ended up converging, so we ended up being able to sandwich the integral of our bounded function between them.
Similarly, we also need an approach to calculate the integral for non-negative functions, so we’ll introduce this lemma:
Lemma 3.2 (Computing integral of non-negative function)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measure space, and a function \(f \in m(\mathcal F, \Sigma)\) is s.t. \(f \geq 0\). Then if \((F_n) \subseteq \mathcal F\) is s.t. \(F_n \uparrow \Omega\) and \(\mu(F_n) < \infty\) for all \(n \in \mathbb N\), then:
Remember that \(f \wedge n\) means \(\min(f, n)\). So, in effect here, what we are doing is “chopping off” \(f\) at a suitable upper bound \(n\) along a \(\mu\)-finite subset of the \(\sigma\)-algebra that is converging (from below) to the event space. The non-negativity assumption of \(f\) suggests that this quantity “should” keep growing; it’s pretty obvious that \(\int_{F_n} f \wedge n \,\text d \mu \leq \int f \,\text d \mu\). The problem is that, along this convergent sequence of sets, we could end up with an accumulation point below the value we are interested in, \(\int f \,\text d \mu\). The purpose of this lemma is to establish that the desired quantity is, in fact, a limit and not just an upper bound.
Proof. Let \(h_n \triangleq (f \wedge n)\mathbb 1_{\{F_n\}}\), and suppose that \(M_n\) is an upper bound for \(h_n\). Note that this upper bound clearly exists, as by construction, \(h_n \leq n\).
It is clear that for each \(h_n \in \left\{0 \leq h \leq f, h \text{ is bounded}, \mu\left(\{\omega \in \Omega : h(\omega) > 0\}\right) < \infty\right\}\), so each \(h_n\) is a possibility for \(h\) in the supremum.
Further, note that \(\int h_n \,\text d \mu\) is a monotone non-decreasing subset, as for every \(n\):
Which follows because \((n + 1) \geq n\), \(F_n \subseteq F_{n + 1}\), and \((f \wedge n + 1) \geq 0\) is upper-bounded by \(M_n\) so Property 3.4 gives that the integral is non-negative.
Suppose that \(h \in \left\{0 \leq h \leq f, h \text{ is bounded}, \mu\left(\{\omega \in \Omega : h(\omega) > 0\}\right) < \infty\right\}\) is an arbitrary element of the supremum set with an upper bound \(M\). Then for any \(n \geq M\), we obtain:
The bottom line follows because \(h_n = f \wedge n\), and \(n \geq M\), so \(h_n \geq f \wedge M\). Further, \(h\) is upper bounded by \(M\) and at most the value of \(f\), so \(h \leq f \wedge M \leq h_n\). Then since \(h \leq h_n\), it follows by Corollary 3.1 that \(\int_{F_n} h \,\text d \mu \leq \int_{F_n} h_n \,\text d \mu\). Continuing and applying Property 3.6:
Which follows by noting that \(h = h \mathbb 1_{\{F_n\}} + h\mathbb 1_{\{F_n^c\}}\), and using the definition of the integral over a set.
Noting that \(0 \leq h \leq M\), then by Corollary 3.1:
Which follows because \(F_n \uparrow \Omega\) implies that \(F_n^c \downarrow \varnothing\), so by convergence from above Property 2.6, \(\mu(F_n^c) \downarrow 0\).
Therefore combining this with (3.3) gives that for every \(h \in \left\{0 \leq h \leq f, h \text{ is bounded}, \mu\left(\{\omega \in \Omega : h(\omega) > 0\}\right) < \infty\right\}\):
3.1.4.1. Properties of the integral for non-negative functions#
At this point, you are probably becoming pretty accustomed to the procedures we are going here. Since we just defined the integral of a non-negative function in terms of bounded functions in Definition 3.8, we’re going to use properties about integrals of bounded functions to prove properties about the integrals of non-negative functions. Let’s get started:
Property 3.7 (Non-negative function has non-negative integral)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f \in m(\mathcal F, \Sigma)\) is s.t. \(f \geq 0\). Then \(\int f \text d \mu \geq 0\).
Proof. Take \(h(\omega) = 0\) for all \(\omega \in \Omega\). Note that \(h \in \left\{h : 0 \leq h \leq f, h \text{ is bounded}, \mu\left(\{\omega \in \Omega : h(\omega) > 0\}\right) < \infty\right\}\).
Further, by Definition 3.2, \(\int h\,\text d \mu = 0\).
Then \(\int f \,\text d \mu \geq \int h\,\text d \mu = 0\), since \(\int f \, \text d\mu\) is a supremum over elements including \(0\).
Well, that one was pretty obvious, let’s try rescaling:
Property 3.8 (Rescaled non-negative function has rescaled integral)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f \in m(\mathcal F, \Sigma)\) is s.t. \(f \geq 0\). Then \(\int rf \,\text d \mu = r\int f \,\text d \mu\).
Proof. If \(r = 0\), the result is immediate, so we’ll consider the case where \(r \neq 0\).
WOLOG suppose that \(r > 0\).
Then using Definition 3.8, for \(r > 0\):
Notice that:
\(q \leq rf \iff \frac{q}{r} \leq f\) for \(r > 0\),
that \(\{q(\omega) > 0\} = \{\frac{q}{r}(\omega) > 0\} \Rightarrow \mu(q > 0) = \mu\left(\frac{q}{r} > 0\right)\), and
\(q\) is bounded by \(M\) \(\iff\) \(\frac{q}{r}\) is bounded by \(\frac{M}{r}\).
Letting \(h \triangleq \frac{q}{r}\) gives:
where we exchanged the integral of the rescaling with the rescaled integral by Property 3.5. Continuing:
This one is also pretty obvious, and basically come down to the fact that we were taking a supremum over what was, effectively, the same set (just rescaled) due to the equivalences and \(\iff\) statements, and then using that \(r > 0\) implied that the supremum of the rescaled values was the rescaling of the supremum of the original values. We could repeat this proof with \(r < 0\) to obtain that the result holds for any \(r\), with suitable adjustments of the inequalities to accomodate the negative values (hence, the WOLOG).
Now, our final aim is summation:
Property 3.9 (Summed non-negative functions have summed integrals)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f, g \in m(\mathcal F, \Sigma)\) are s.t. \(f, g \geq 0\). Then \(\int (f + g)\,\text d \mu = \int f \,\text d \mu + \int g \,\text d \mu\).
We’ll address this by showing that Left \(\leq\) RHS, and RHS \(\leq\) LHS, and therefore RHS \(=\) LHS:
Proof. 1. \(\int (f + g)\,\text d \mu \leq \int f \,\text d \mu + \int g \,\text d \mu\):
Note that \((a + b)\wedge n \leq (a \wedge n) + (b \wedge n)\).
Let \((F_n) \subseteq \mathcal F\) be a \(\mu\)-finite sequence where \(F_n \uparrow \Omega\) from below. Then:
which is because \((f \wedge n) \mathbb 1_{F_n}\) and \((g \wedge n) \mathbb 1_{F_n}\) are bounded, so application of Property 3.6 gives the desired result. Then by Lemma 3.2:
2. \(\int (f + g)\,\text d \mu \geq \int f \,\text d \mu + \int g \,\text d \mu\):
Suppose that \(h \in \{h : 0 \leq h \leq f,h \text{ is bounded}, \mu(h > 0) < \infty\}\), and that \(k \in \{k : 0 \leq k \leq g,k \text{ is bounded}, \mu(k > 0) < \infty\}\). Then by definition, it follows that \(h \leq f, k \leq g\), so \(h + k \leq f + g\).
Therefore:
So:
which follows by the Definition 3.8, the integral of a non-negative function.
As before, since non-negative functions obey inequalities with respect to \(0\), are rescalable by \(-1\), and their sums have summed integrals, we obtain all of the integration corollaries in Section 3.1.2.
We are now ready to relax the class of functions we can integrate to the broadest class of functions we will deal with in this course: the integrable functions.
3.1.5. \(\mu\)-integrable functions#
Let’s start with a quick definition:
Definition 3.9 (\(\mu\)-integrable functions)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, and \((\mathbb R, \Sigma)\) is a measurable space. We say that \(f \in m(\mathcal F, \Sigma)\) is \(\pmb\mu\)-integrable if \(\int |f| \,\text d \mu < \infty\).
Like before, we’ll now start with a definition of an integral for a \(\mu\)-integrable function:
Definition 3.10 (Integral of a \(\mu\)-integrable function)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f \in m(\mathcal F, \Sigma)\) is \(\mu\)-integrable, and for each \(\omega \in \Omega\), define:
Then the integral is:
It should be pretty immediately clear to you that for every \(\omega \in \Omega\), that \(f(\omega) = f^+(\omega) - f^-(\omega)\), and that \(|f(\omega)| = f^+(\omega) + f^-(\omega)\), just by construction. Another pretty easy interesting note to conclude that \(f^+(\omega), f^-(\omega) \leq |f(\omega)|\).
Since \(f^+ \geq 0\) and \(f^- \geq 0\), by Definition 3.8 and Corollary 3.1 if \(f\) is \(\mu\)-integrable:
Just by looking off at the Definition 3.9 for a \(\mu\)-integrable function, which also directly that the quantity is well-defined.
3.1.5.1. Properties of \(\mu\)-integrable functions#
Well, this time we know that we can compute the integral using mt:int:basics:muint:compute, as well as the corresponding discussion that we had. But we still need some more machinery to show that our basic properties of integration hold like before:
Lemma 3.3 (Integral of a difference)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f \in m(\mathcal F, \Sigma)\) is \(\mu\)-integrable, where \(f = f_1 - f_2\), and \(f_1, f_2 \geq 0\), where for each \(i \in \{1, 2\}\), \(\int f_i \,\text d \mu < \infty\). Then:
Proof. Note that with \(f^+, f^-\) as defined above, that \(f = f^+ - f^- = f_1 - f_2\). Then:
where \(f^+, f^-, f_1, f_2 \geq 0\).
Then by repeatedly applying Corollary 3.2 for non-negative functions and Property 3.9:
Since RHS is the definition of a \(\mu\)-integrable function’s integral, Definition 3.10.
And now, onto our properties. This first one seems extremely obvious, but as it turns out, it requires a little bit of nuance. We’ll introduce a general purpose lemma here, which will let us handle this in the future:
Lemma 3.4 (Integral of non-negative function on a \(\mu\)-null set is \(0\))
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f \in m(\mathcal F, \Sigma)\) is non-negative. Then if \(F\) is a \(\mu\)-null set, \(\int_{F} f \,\text d \mu = 0\).
Proof. Recall that \(\int_{\{F\}} f \,\text d \mu \triangleq \int f\mathbb 1_{\{F\}} \,\text d \mu\), by Definition 3.7.
With \(h \triangleq f \mathbb 1_{\{F\}}\), note that the integral of \(f\) itself is defined as a supremum over bounded functions by Definition 3.8, which are defined as a supremum over simple functions by Theorem 3.1.
Suppose that \(\varphi\) is any such simple function, and let \(\{(\alpha_n, E_n)\}_{n \in [N]} \subseteq \mathcal F\) be the coefficients/disjoint sets with which each are defined, by Definition 3.2.
Note that with \(h \triangleq f \mathbb 1_{\{F\}}\), that the simple functions which are used to define the integral of \(h\) will be \(\varphi \mathbb 1_{\{F\}}\), and will have coefficients/disjoint sets \(\{(\alpha_n, E_n \cap F)\}_{n \in [N]}\). However, for every such simple function:
because \(0 \leq \mu(E_n \cap F) \leq \mu(F) = 0\).
Working back upwards, all of the simple functions, all of the bounded functions, and consequently \(h\) will have an integral \(0\).
And we can extend it extremely trivially to \(\mu\)-integrable functions, too (try it!):
Corollary 3.4 (Integral of \(\mu\)-integrable function on a \(\mu\)-null set is \(0\))
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f \in m(\mathcal F, \Sigma)\) is \(\mu\)-integrable. Then if \(F\) is a \(\mu\)-null set, \(\int_{F} f \,\text d \mu = 0\).
Since bounded and simple functions are special cases of \(\mu\)-integrable functions, the machinery will readily apply to those cases, too.
Now, we are ready to handle the properties:
Property 3.10 (Non-negative \(\mu\)-integrable function has non-negative integral)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, and \(f \in m(\mathcal F, \Sigma)\) is \(\mu\)-integrable where \(f \overset{a.e.}{\geq} 0\). Then \(\int f \,\text d \mu \geq 0\).
Proof. Let \(F^c\) be the \(\mu\)-null set on which \(f(\omega) < 0\), and define \(f^+\) and \(f^-\) as in Definition 3.10. By construction, note that \((f^-) \mathbb 1_{\{F^c\}} \equiv f^- \geq 0\). Then by Lemma 3.4:
Then:
which is by Property 3.7 since \(f^+ \geq 0\).
We can rescale them:
Property 3.11 (Rescaled \(\mu\)-integrable functions have rescaled integrals)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, \(f \in m(\mathcal F, \Sigma)\) is \(\mu\)-integrable, and \(r \in \mathbb R\). Then \(\int r f \,\text d \mu = r \int f \,\text d \mu\).
Proof. Define \(f^+\) and \(f^-\) as in Definition 3.10. Note that since \(f^+\) and \(f^-\) are non-negative, then by Property 3.9:
where the second-to-last line follows by Property 3.8.
and finally, we can sum them:
Property 3.12 (Summed \(\mu\)-integrable functions have summed integral)
Suppose that \((\Omega, \mathcal F, \mu)\) is a measure space, \((\mathbb R, \Sigma)\) is a measurable space, \(f,g \in m(\mathcal F, \Sigma)\) is \(\mu\)-integrable. Then \(\int (f + g)\,\text d \mu = \int f \,\text d \mu + \int g \,\text d \mu\).
Proof. Define \(f^+, f^-, g^+, g^-\) as in Definition 3.10. Note that:
Where \((f^+ + g^+), (f^- + g^-) \geq 0\), and further, have finite integrals since \(f, g\) are \(\mu\)-integrable, the sum of non-negative functions are non-negative, and then application of (3.4).
Note further that \(|f + g| \leq |f| + |g|\) by the triangle inequality, so \(f, g\) \(\mu\)-integrable implies that \(f + g\) is \(\mu\)-integrable. Then by Lemma 3.3:
which is because \(f^+, g^+, f^-, g^- \geq 0\) by Property 3.9. Simply rearranging terms:
since these are their definitions given by Definition 3.10.
As always, we obtain all of the integration corollaries in Section 3.1.2 due to these three properties holding for \(\mu\)-integrable functions.
Remark 3.1 (Constant functions follow all the properties discussed)
Suppose that you have an extremely simple function; e.g., \(f(\omega) = x\), where \(x \in \mathbb R\) is a constant. This function is certainly simple; e.g., take \(\alpha_n = x\), \(F_1 = \Omega\). It should be pretty clear to you that because it is simple, it is obviously bounded (you can use the number \(x\) itself as the bound), it is a rescaling of a non-negative function (if \(x < 0\), consider that \(f(\omega) = -g(\omega)\), where \(g(\omega) = -x \geq 0\)), and it is therefore integrable too, assuming that the measure of the whole space is finite.
Think about this remark a little bit.
